Логическая функция F задается...

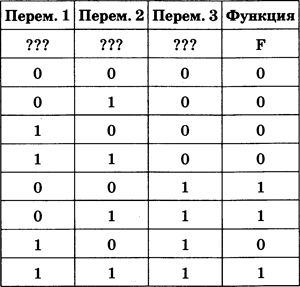
Логическая функция F задается выражением $ (¬ x) \wedge y \vee y \wedge z $ . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных х,y,z.

В ответе напишите буквы х,y,z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая 1-му столбцу, затем — буква, соответствующая 2-му столбцу, затем — буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

$ \wedge $ - логическое умножение (конъюнкция) , можно заменить на И.
$ \vee $-логическое сложение (дизъюнкция), можно заменить на ИЛИ.

1)Упростим выражение по закону дистрибутивности $ A\wedge B \vee A\wedge C = A\wedge(B\vee C) $
\[ (¬x) \wedge y \vee y \wedge z= y\wedge(¬(x)\vee z)=F \]
2)В первых четырёх строчках функция равна нулю.
\[(¬x) \wedge y \vee y \wedge z= y\wedge(¬(x)\vee z)=0\]
Для того чтобы равенство выполнялось y или $(¬(x)\vee z)$ должны быть равны 0.
$y=0$ или $ (¬(x)\vee z)=0 $

Столбик в котором y=0 в четырёх первых строчках под номером три (y - третий столбец).

3) В последних четырёх строчках y=1, поэтому его можно убрать (A*1=A). Получим $(¬(x)\vee z)=F $
Рассмотрим когда F=0.
$(¬(x)\vee z)=0$

Данное выражение равно нулю только при x=1 и z=0.
Соответственно x первый столбик, а z второй.