В треугольнике $ABC$ известны длины...

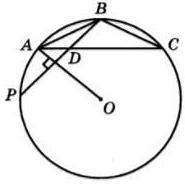
В треугольнике $ABC$ известны длины сторон $AB=60$, $AC=80$, точка $O$-центр окружности, описанной около треугольника $ABC$. Прямая $BD$, перпендикулярная прямой $AO$, пересекает $AC$ в точке $D$. Найдите $CD$.

Пусть продолжение отрезка $BD$ за точку $D$ пересекает окружность, описанную около треугольника $ABC$ в точке $P$(см. рис.). Тогда хорда $BP$ перпендикулярна радиусу $OA$ этой окружности. Значит, точка $A$ - середина дуги $BP$, не содержащей вершину $C$. Отсюда следует, что $\angle ABD=\angle ABP=\angle ACB$ (как вписанные углы, опирающиеся на равные дуги). Поэтому треугольники $ABD$ и $ACB$ подобны по двум углам (угол $A$ - общий).

Следовательно, $\frac{AD}{AB}=\frac{AB}{AC}$,

откуда $AD=\frac{AB^{2}}{AC}=45$ и $CD=AC-AD=80-45=35$.

Ответ: $35$.