В треугольнике $ABC$ биссектриса...

В треугольнике $ABC$ биссектриса угла $A$ делит высоту, проведенную из вершины $B$, в отношении $13:12$, считая от точки $B$. Найдите радиус окружности, описанной около треугольника $ABC$, если $BC=20$.

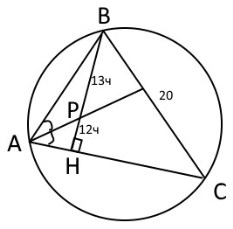
$BH$ -высота, $AP$-биссектриса(см. рис.)

Из треугольника $ABH$: так как $AP$-биссектриса, то

$\frac{AH}{AB}=\frac{PH}{PB}=\frac{12}{13}$;

$cos BAH=\frac{AH}{AB}$.

Следовательно, $cos BAH=\frac{12}{13}$.


Тогда $sin BAH=\sqrt{1-(cos BAH)^{2}}=\sqrt{1-(\frac{12}{13})^{2}}=\frac{5}{13}$.

$\frac{a}{sin \alpha}=2R$, где $a$-сторона треугольника, $\alpha$-противолежащий ей угол, $R$-радиус описанной окружности.

Значит, $R=\frac{a}{2sin \alpha}=\frac{BC}{2sin BAH}=\frac{20}{2\cdot \frac{5}{13}}=26$.

Ответ: $26$