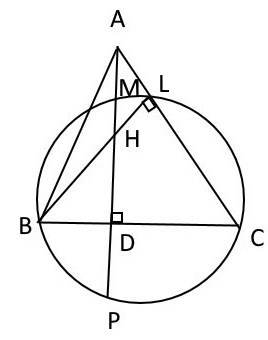
На стороне $BC$ остроугольного...

На стороне $BC$ остроугольного треугольника $ABC$ как на диаметре построена полуокружность, пересекающая $AD$ в точке $M$, $AD=90$, $MD=69$, $H$ - точка пересечения высот треугольника $ABC$. Найдите $AH$.

Построим угол $BLC$, так как он опирается на диаметр $BC$ окружности, то он будет прямой.

Значит, $BL$-высота.

То есть $AD$(высота по условию) пересекает $BL$ в точке $H$.

Продолжим прямую $AD$ до пересечения с окружностью во второй точке $P$.

Так как хорда $MP$ перпендикулярна диаметру $BC$, то $MD=PD=69$.

По свойству секущих получаем:

$AM\cdot AP=AL\cdot AC=(90-69)\cdot (90+69)=3339$

Треугольники $ALH$ и $ADC$ подобны по двум углам(угол $DAC$-общий, углы $ALH$ и $ADC$ - прямые)

=> $\frac{AL}{AD}=\frac{AH}{AC}$

$AH=\frac{AL\cdot AC}{AD}=\frac{3339}{90}=37,1$

Ответ: $37,1$