На числовой прямой даны два отрезка:...

На числовой прямой даны два отрезка: $P = [27; 60]$ и $Q = [45; 62]$. Укажите наименьшую возможную длину такого отрезка $A$, что формула

$((x\in P)\rightarrow ((x\in Q)\wedge ¬(x\in A))) \rightarrow ¬(x\in P)$

истинна при любом значении переменной $x$, т.е. принимает значение 1 при любом значении переменной $x$.

Упростим выражение и заменим $(x\in P)$ на P и т.д.

$P\rightarrow (Q\wedge ¬ A)\rightarrow P=1$

*$A\rightarrow B=¬ A\vee B$
*$¬ (A\wedge B)=¬ A\vee ¬ B$

$¬ P \vee ¬ Q\vee A¬ P$

*$A\wedge A=A$ и $A\vee A=A$

$¬Q \vee ¬ P\vee A$

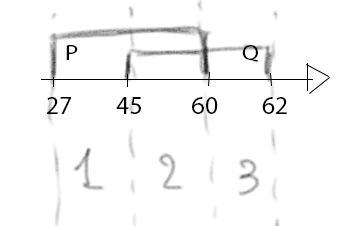
На числовой прямой отметим P и Q, а также разобьём на три интервала как показано на рисунке.

1)Q=0, P=1. Поставляем
1+A+0=1 - не зависит от А
2)Q=0, P=0
0+А+0=1 - А обязательно должна принадлежать второму интервалу [45;60]
3)Q=1, P=0
0+A+1=1 - не зависит от А

60-45=15