На карту нанесены 4 города (A, В, С...

На карту нанесены 4 города (A, В, С и D).

Известно, что:

между городами А и С — три дороги,
между городами С и В — две дороги,
между городами А и В — две дороги,
между городами С и D — две дороги,
между городами В и D — четыре дороги.

По каждой из этих дорог можно ехать в обе стороны. Сколькими различными способами можно проехать из А в D, посещая каждый город не более одного раза?

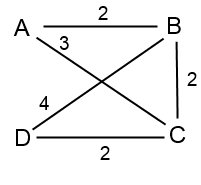
Построим схему соединения всех дорог (см рис) и переборем все возможные варианты добраться из пункта A в пункт D.

$A \rightarrow B \rightarrow D$ (2*4 = 8 способов)

$A \rightarrow B \rightarrow C \rightarrow D$ (2*2*2 = 8 способов)

$A \rightarrow C \rightarrow D$ (6 способов)

$A \rightarrow C \rightarrow B \rightarrow D$ (24 способа)

Итого имеем: $8+8+6+24 = 46$ способов.