ЕГЭ по Математике (базовый)
Прямые $m$ и $n$ параллельны....
Задание:
Прямые $m$ и $n$ параллельны. Найдите $\angle 3$, если $\angle 1=77^{\circ}$, $\angle 2=88^{\circ}$. Ответ дайте в градусах.
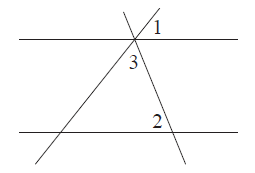
Решение:
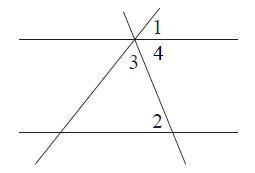
Обозначим еще один угол - угол 4 (см. рисунок ниже). Данный угол с углом 1 и 3 образуют развернутый угол (прямая линия) и их сумма будет равна 180 градусам: $\angle 1+\angle 3+\angle 4=180^{\circ}$.
Нам неизвестен угол 4. Внимательно посмотрев на рисунок, можно заметить, что угол 2 и 4 являются накрест-лежащими, а значит они равны.
Найдём угол 3:
\[77^{\circ}+\angle 3+88^{\circ}=180^{\circ}\]
\[\angle 3=180^{\circ}-77^{\circ}-88^{\circ}\]
\[\angle 3=15^{\circ}\]
Нам неизвестен угол 4. Внимательно посмотрев на рисунок, можно заметить, что угол 2 и 4 являются накрест-лежащими, а значит они равны.
Найдём угол 3:
\[77^{\circ}+\angle 3+88^{\circ}=180^{\circ}\]
\[\angle 3=180^{\circ}-77^{\circ}-88^{\circ}\]
\[\angle 3=15^{\circ}\]
Ответ:
15
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Базовый уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
