ЕГЭ по Математике (базовый уровень)
Зарегистрируйтесь и Ваши результаты будут сохраняться.
Прочтите:
Вариант был составлен автоматически, аналогично демоверсии реального экзамена.
На каждую позицию было подобрано случайное типовое задание из нашей базы данных.
Каждое задание имеет решение, которое будет показано после выполнения работы.
Задания с развернутым ответом не провяряются автоматически. После выполнения работы проверьте себя сами.
В ответ записывайте ТОЛЬКО целые числа и десятичные дроби (через запятую).
Выполняйте вариант честно. Для себя. Вы ни с кем не соревнуетесь. Кнопка проверить вариант находится внизу.
Удачи!
Каждое задание имеет решение, которое будет показано после выполнения работы.
Задания с развернутым ответом не провяряются автоматически. После выполнения работы проверьте себя сами.
В ответ записывайте ТОЛЬКО целые числа и десятичные дроби (через запятую).
Выполняйте вариант честно. Для себя. Вы ни с кем не соревнуетесь. Кнопка проверить вариант находится внизу.
Удачи!
Ваш результат:
Вы вполнили правильно из .
Задания с развернутым ответом проверьте самостоятельно.
Ваш результат сохранен в Вашем профиле.
После перезагрузки страницы система составит новый вариант.
Задание 1
Найдите значение выражения $\frac{13}{7}\div \frac{26}{35}-1,5.$
Задание 2
Найдите значение выражения $3\cdot 4^{3}+2\cdot 4^{3}$.
Задание 3
Набор полотенец, который стоил 250 рублей, продается со скидкой 7%. Сколько рублей стоят два набора полотенец со скидкой?
Задание 4
Закон Гука можно записать в виде $F=kx$, где $F$ — сила (в ньютонах), с которой сжимают пружину, $x$ — абсолютное удлинение (сжатие) пружины (в метрах), а $k$ — коэффициент упругости. Пользуясь этой формулой, найдите $x$ (в метрах), если $F=38$ H и $k=2$ H/м.
Задание 5
Найдите значение выражения $2^{log_{2}7+3}$.
Задание 6
Стоимость проездного билета на месяц составляет 690 рублей, а стоимость билета на одну поездку - 26 рублей. Аня купила проездной и сделала за месяц 35 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?
Задание 7
Найдите корень уравнения $log_{4}(2x+5)=3.$
Задание 8
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
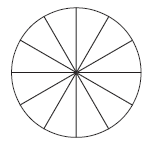
Задание 9
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

Задание 10
Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Задание 11
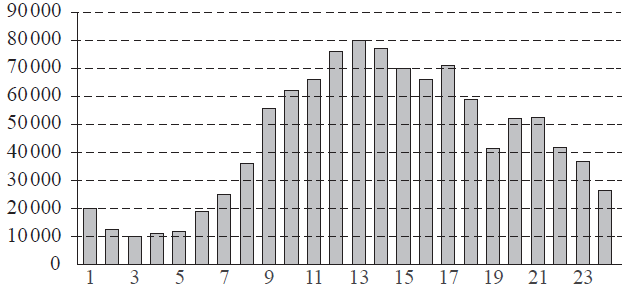
На диаграмме показано количество посетителей сайта РИА «Новости» в течение каждого часа 8 декабря 2009 года. По горизонтали указывается час, по вертикали — количество посетителей сайта на протяжении этого часа. Определите по диаграмме, в течение какого часа на сайте РИА «Новости» побывало минимальное количество посетителей.
Задание 12
Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 600 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды, клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива - 25 рублей за литр, бензина - 35 рублей за литр, газа - 20 рублей за литр. Сколько рублей заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
Задание 13
Однородный шар диаметром 2 см имеет массу 48 г. Чему равна масса шара, изготовленного из того же материала, с диаметром 3 см? Ответ дайте в граммах.
Задание 14
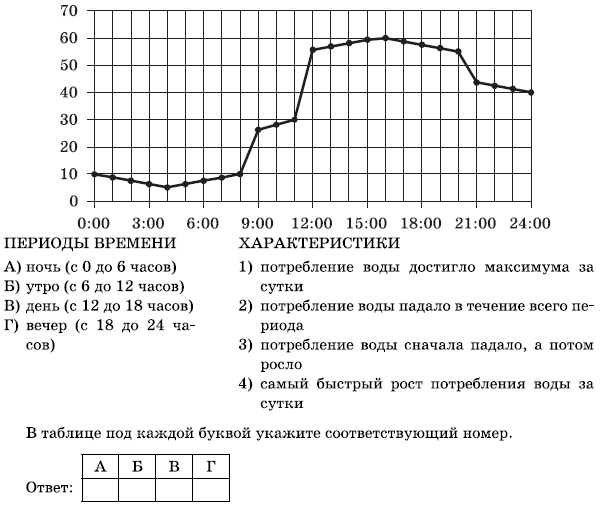
На рисунке точками показано потребление воды городской ТЭЦ на протяжении суток. По горизонтали указываются часы, по вертикали — объём воды в кубометрах. Для наглядности точки соединены линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику потребления воды данной ТЭЦ в течение этого периода.
Задание 15
В параллелограмме $ABCD$ диагональ $AC$ в 2 раза больше стороны $AB$ и $\angle ACD=74^{\circ}$. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
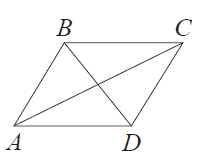
Задание 16
Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 20. Найдите площадь боковой поверхности этой пирамиды.
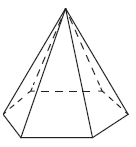
Задание 17
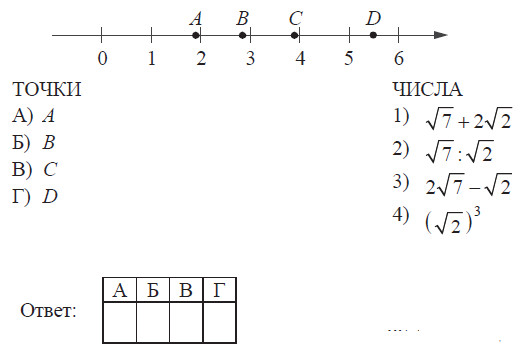
На координатной прямой отмечены точки $A$, $B$, $C$ и $D$. Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.
Задание 18
Среди жителей дома № 23 есть те, кто работает, и есть те, кто учится. А также есть те, кто не работает и не учится. Некоторые жители дома № 23, которые учатся, ещё и работают. Выберите утверждения, которые верны при указанных условиях.
1) Хотя бы один из работающих жителей дома № 23 учится.
2) Все жители дома № 23 работают.
3) Среди жителей дома № 23 нет тех, кто не работает и не учится.
4) Хотя бы один из жителей дома № 23 работает.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Хотя бы один из работающих жителей дома № 23 учится.
2) Все жители дома № 23 работают.
3) Среди жителей дома № 23 нет тех, кто не работает и не учится.
4) Хотя бы один из жителей дома № 23 работает.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Задание 19
Приведите пример трехзначного числа $A$, обладающего следующими свойствами:
- сумма цифр числа $A$ делится на 8;
- сумма цифр числа $A+1$ также делится на 8;
- в числа $A$ сумма крайних цифр кратна средней цифре.
В ответ укажите ровно одно такое число.
- сумма цифр числа $A$ делится на 8;
- сумма цифр числа $A+1$ также делится на 8;
- в числа $A$ сумма крайних цифр кратна средней цифре.
В ответ укажите ровно одно такое число.
Ответ к этому заданию автоматически не проверяется
Задание 20
На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса? Меридиан – это дуга окружности, соединяющая Северный и Южный полюса. параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора.
TOP 5 сегодня | ЕГЭ
Еще никто не готовится - начни первый!