Стороны основания правильной...

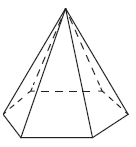
Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 20. Найдите площадь боковой поверхности этой пирамиды.

Так как пирамида правильная, то в основании правильный шестиугольник, значит, все стороны основания между собой равны и боковая поверхность пирамиды состоит из шести равных равнобедренных треугольников, основания которых 24, а стороны - 20.

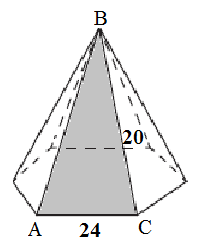
Для начала найдём площадь одной боковой грани. Для этого рассмотрим равнобедренный треугольник ABC (см. рисунок ниже). Мы знаем, что площадь равнобедренного треугольника равна произведению высоты на половину длины основания $S=\frac{1}{2}\cdot a\cdot h$. Длину основания мы знаем, необходимо найти высоту.

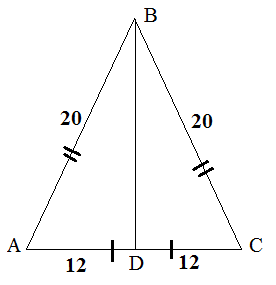
В треугольнике ABC мы знаем основание, оно равно 24. Проведем высоту к основанию, так как треугольник равнобедренный, то высота является и медианой, значит, она делит основание пополам. Следовательно, AD = DC = 12. По теореме Пифагора найдем высоту BD:
\[AB^{2}=BD^{2}+AD^{2}\]
\[20^{2}=BD^{2}+12^{2}\]
\[BD^{2}=256\]
\[BD=16.\]

Теперь подставим численные значения в формулу для нахождения площади равнобедренного треугольника:
\[S=\frac{1}{2}\cdot 16\cdot 24=192.\]

Ранее писали, что боковая поверхность пирамиды состоит из шести равных равнобедренных треугольников, значит, чтобы найти площадь боковой поверхности пирамиды, нам необходимо умножить площадь равнобедренного треугольника (одна боковая поверхность) на 6: $192\cdot 6=1152.$