В параллелограмме $ABCD$ диагональ...

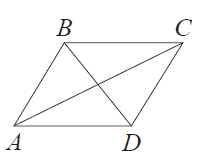
В параллелограмме $ABCD$ диагональ $AC$ в 2 раза больше стороны $AB$ и $\angle ACD=74^{\circ}$. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

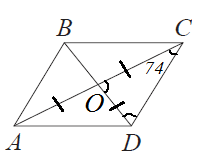
Мы знаем, что $AB=CD$. По условию, $AC=2AB$ и значит $AC=2CD$. Одно из свойств параллелограмма гласит: диагонали параллелограмма точкой пересечения делятся пополам. Пусть, точка пересечения диагоналей будет т.O (см. рисунок ниже), тогда, $CO=\frac{1}{2}AC=CD$. Так как $AC=2AB=2CD$ и $OC=CD$, следовательно, треугольник $COD$ равнобедренный и угол $COD$ равен углу $CDO$.

Мы знаем, что сумма углов в треугольнике равна 180 градусов. Применим данное свойство:
\[\angle COD+\angle CDO+\angle OCD=180^{\circ}\].
Пусть, $\angle COD=\angle CDO=\alpha$. Тогда получим уравнение и найдем чему равен угол между диагоналями, то есть угол $COD$:
\[\alpha +\alpha +74^{\circ}=180^{\circ}\]
\[2\alpha =106^{\circ}\]
\[\alpha =53^{\circ}.\]