В прямоугольном параллелепипеде...

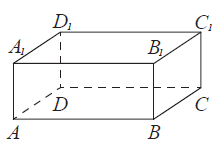
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ рёбра $AB$, $AD$ и диагональ $AB_{1}$ равны соответственно 4, 7 и $\sqrt{41}$. Найдите объём параллелепипеда $ABCDA_{1}B_{1}C_{1}D_{1}$.

Чтобы найти объём прямоугольного параллелепипеда необходимо умножить длину на ширину и на высоту $V=a\cdot b\cdot c$. Нам известна длина $AB$, ширина $AD$, но неизвестна высота.

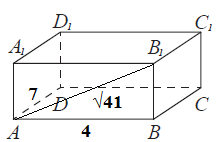
Найдём высоту $B_{1}B$ из прямоугольного треугольника $AB_{1}B$ (см. рисунок ниже) по теореме Пифагора:
\[AB_{1}^{2}=AB^{2}+BB_{1}^{2}\]
\[\left (\sqrt{41} \right )^{2}=4^{2}+BB_{1}^{2}\]
\[BB_{1}^{2}=41-16\]
\[BB_{1}^{2}=25\]
\[BB_{1}=5.\]
Подставим численные значения в формулу нахождения объёма прямоугольного параллелепипеда и найдём объём:
\[V=4\cdot 7\cdot 5=140.\]