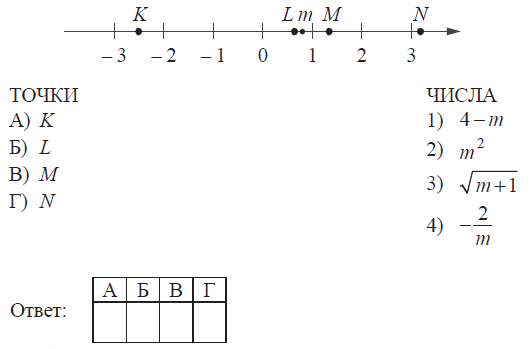
На координатной прямой отмечено...

На координатной прямой отмечено число $m$ и точки $K$, $L$, $M$ и $N$. Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.

На координатной прямой видно, что число $m$ примерно равно 0,8.

Рассмотрим числа, какие у нас присутствуют. Начнем с числа $4-m$: мы знаем, что $m\approx 0,8$, значит, $4-m=4-0,8\Rightarrow 4-m=3,2$. Данное число на координатной прямой должно стоять правее тройки, по координатной прямой видно, что правее тройки находится только точка $N$. Значит, Г) - 1)

Следующее число $m^{2}$. 0,8 в квадрате равен 0,64. Данная точка должна быть примерно между 1 и 0. В этом промежутке только одна точка - точка $L$. Значит, Б) - 2)

Далее идет число $\sqrt{m+1}$. Подставим вместо $m$ число 0.8: $\sqrt{0,8+1}=\sqrt{1,8}\approx 1,34$. Правее единицы только точка $M$. Значит, В) - 3)

Осталось еще одно число - $-\frac{2}{m}$ и одна точка - $K$. Проверим, удовлетворяет ли данная точка этому числу, подставив 0,8 вместо $m$: $-\frac{2}{0,8}=-2,5$. Точка $K$ находится посередине -3 и -2, а нас получилось -2,5, таким образом, данная точка удовлетворяет этому числу. Значит, А) - 4)

Таким образом, ответ будет выглядеть следующим образом: 4231.