ЕГЭ по Математике (базовый)
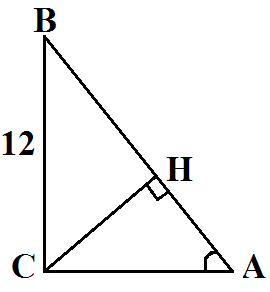
В треугольнике $ABC$ угол $C$ равен...
Задание:
В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $BC=12$, $cosA=0,25$. Найдите высоту $CH$.
Решение:
Высота - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону (см. рисунок ниже).
В треугольнике $BCH$ у нас известна гипотенуза $BC$. Мы знаем, что синус - отношение противолежащего катета к гипотенузе. Косинус - отношение прилежащего катета к гипотенузе. В нашем случае $cosA=\frac{AC}{AB} ; cosB=\frac{AC}{AB}$, получается, что $cosA=sinB$.
В треугольнике $BCH$: $sinB=\frac{HC}{BC}$. Подставим значения:
\[0,25=\frac{HC}{12}\]
\[HC=3.\]
В треугольнике $BCH$ у нас известна гипотенуза $BC$. Мы знаем, что синус - отношение противолежащего катета к гипотенузе. Косинус - отношение прилежащего катета к гипотенузе. В нашем случае $cosA=\frac{AC}{AB} ; cosB=\frac{AC}{AB}$, получается, что $cosA=sinB$.
В треугольнике $BCH$: $sinB=\frac{HC}{BC}$. Подставим значения:
\[0,25=\frac{HC}{12}\]
\[HC=3.\]
Ответ:
3
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Базовый уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
