На координатной прямой отмечены...

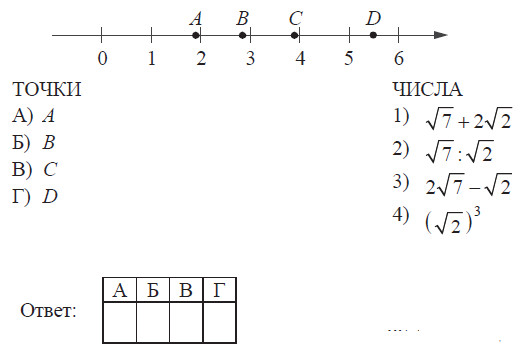
На координатной прямой отмечены точки $A$, $B$, $C$ и $D$. Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.

Впишите в приведённую в ответе таблицу под каждой буквой соответствующий числу номер.

Число $\sqrt{7}$ - число между $\sqrt{4}$ и $\sqrt{9}$. $\sqrt{4}=2$, $\sqrt{9}=3$. $\sqrt{7}$ чуть ближе к 9, значит $\sqrt{7}$ немного больше, чем 2,5 и примерно равно 2,65. А то что $\sqrt{2}\approx 1,4$ мы все знаем.

Посчитаем каждое число по отдельности:

1) $\sqrt{7}+2\sqrt{2}\approx2,65+2\cdot 1,4\approx5,54$

2) $\sqrt{7}\div \sqrt{2}\approx2,65\div 1,4\approx 1,9$

3) $2\sqrt{7}-\sqrt{2}\approx 2\cdot 2,65-1,4\approx 3,9$

4) $\left (\sqrt{2} \right )^{3}\approx \sqrt{2}\cdot \sqrt{2}\cdot \sqrt{2}\approx 2\cdot \sqrt{2}\approx2\cdot 1,4\approx2,8$

1,9 < 2,8 < 3,9 < 5,54. На координатной прямой левее всех точка A, значит ему соответствует значение 1,9, т.е. 2). Дальше идет точка B, значит это число 2,8, т.е. 4). Аналогично точке C соответствует число 3) и точке D - 1).

Таким образом получаем ответ: 2431.