ЕГЭ по Математике (базовый)
В угол $C$, равный $68^{\circ}$,...
Задание:
В угол $C$, равный $68^{\circ}$, вписана окружность с центром $O$, которая касается сторон угла в точках $A$ и $B$. Найдите угол $AOB$. Ответ дайте в градусах.
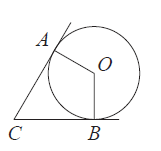
Решение:
Первое решение:
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы $CAO$ и $CBO$ прямые, т.е. по $90^{\circ}$. В четырехугольнике $AOBC$ сумма углов равна $360^{\circ}$, значит, угол $AOB$ будет равен $360^{\circ}-90^{\circ}-90^{\circ}-83^{\circ}=112^{\circ}$.
Второе решение:
Углы $CAO$ и $CBO$ прямые, так как $OA$ и $OB$ радиусы проведенные к касательным. $CO$ - биссектриса, так как равноудалена от сторон угла, а биссектриса делит угол пополам, это значит, что угол $OCB$ равен $68^{\circ}\div 2=34^{\circ}$.
Найдем угол $COB$ из прямоугольного треугольника $COB$, при этом мы знаем, что сумма углов в треугольнике равна $180^{\circ}$: $180^{\circ}-34^{\circ}-90^{\circ}=56^{\circ}$. А ранее мы писали, что биссектриса делит угол пополам, значит, угол $AOB$ будет равен $56^{\circ}\cdot 2=112^{\circ}$.
Радиус окружности перпендикулярен касательной в точке касания, поэтому углы $CAO$ и $CBO$ прямые, т.е. по $90^{\circ}$. В четырехугольнике $AOBC$ сумма углов равна $360^{\circ}$, значит, угол $AOB$ будет равен $360^{\circ}-90^{\circ}-90^{\circ}-83^{\circ}=112^{\circ}$.
Второе решение:
Углы $CAO$ и $CBO$ прямые, так как $OA$ и $OB$ радиусы проведенные к касательным. $CO$ - биссектриса, так как равноудалена от сторон угла, а биссектриса делит угол пополам, это значит, что угол $OCB$ равен $68^{\circ}\div 2=34^{\circ}$.
Найдем угол $COB$ из прямоугольного треугольника $COB$, при этом мы знаем, что сумма углов в треугольнике равна $180^{\circ}$: $180^{\circ}-34^{\circ}-90^{\circ}=56^{\circ}$. А ранее мы писали, что биссектриса делит угол пополам, значит, угол $AOB$ будет равен $56^{\circ}\cdot 2=112^{\circ}$.
Ответ:
112
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Базовый уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
