ЕГЭ по Математике (базовый)
В треугольнике $ABC$ известно, что...
Задание:
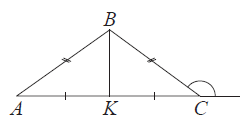
В треугольнике $ABC$ известно, что $AB=BC=24$, внешний угол при вершине $C$ равен $150^{\circ}$. Найдите длину медианы BK.
Решение:
Развернутый угол равен $180^{\circ}$, значит, внутренний угол $C$ равен $180^{\circ}-30^{\circ}=150^{\circ}$.
Так как, треугольник $ABC$ - равнобедренный ($AB=AC$), то и углы при вершинах $A$ и $C$ равны. Если опустить медиану $BK$, то она будет являться так же и высотой (по свойству медианы в равнобедренном треугольнике).
Рассмотрим прямоугольный треугольник $BCK$, где $BC$ - гипотенуза, $BK$ и $CK$ - катеты. Учтем, что $BK=0,5\cdot BC$, потому что катет лежащий на против угла в $30^{\circ}$ равен половине гипотенузы. Получается, что медиана $BK$ равна $0,5\cdot 24=12.$
Так как, треугольник $ABC$ - равнобедренный ($AB=AC$), то и углы при вершинах $A$ и $C$ равны. Если опустить медиану $BK$, то она будет являться так же и высотой (по свойству медианы в равнобедренном треугольнике).
Рассмотрим прямоугольный треугольник $BCK$, где $BC$ - гипотенуза, $BK$ и $CK$ - катеты. Учтем, что $BK=0,5\cdot BC$, потому что катет лежащий на против угла в $30^{\circ}$ равен половине гипотенузы. Получается, что медиана $BK$ равна $0,5\cdot 24=12.$
Ответ:
12
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Базовый уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
