В треугольнике $ABC$ известно, что...

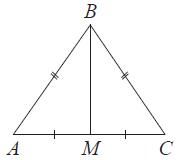
В треугольнике $ABC$ известно, что $AB=BC$, медиана $BM$ равна 6. Площадь треугольника $ABC$ равна $12\sqrt{7}$. Найдите длину стороны $AB$.

Площадь треугольника равна половине произведения основания на высоту $S_{ABC}=\frac{1}{2}\cdot AC\cdot BM$. Откуда найдем основание $AC$:
\[AC=\frac{2\cdot S_{ABC}}{BM}=\frac{2\cdot 12\sqrt{7}}{6}=4\sqrt{7}\].

Так как треугольник $ABC$ равнобедренный (по условию $AB=BC$), то медиана делит основание пополам, т.е. $AM=\frac{1}{2}\cdot AC=\frac{1}{2}\cdot 4\sqrt{7}=2\sqrt{7}$.

Рассмотрим прямоугольный треугольник $ABM$, где известны катеты $AM$ и $BM$. По теореме Пифагора найдем гипотенузу $AB$:
\[AB^{2}=AM^{2}+BM^{2}\]
\[AB^{2}=\left (2\sqrt{7} \right )^{2}+6^{2}\]
\[AB^{2}=28+36=64\]
\[AB=8.\]