Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ). У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования. Обо всем по порядку расскажу тебе после быстрой регистрации.

Олимпиада «Шаг в будущее» Математика 11 класс II этап

Задание 1. Задача 1 (0/1)

Задание 2. Задача 2 (0/1)

Задание 3. Задача 3 (0/1)

Задание 4. Задача 4 (0/1)

Задание 5. Задача 5 (0/1)

Задание 7. Задача 7 (0/1)

Задание 6. Задача 6 (0/1)

Задание 8. Задача 8 (0/1)

Задание 9. Задача 9 (0/1)

Задание 10. Задача 10 (0/1)

Боковые ребра треугольной пирамиды...

Задание:

Боковые ребра треугольной пирамиды $TABC$ образуют между собой прямые углы. Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через вершину $C$ и середину стороны $AB$ основания, если сторона основания $AC = 5$ и боковые ребра $TA = 4, TB = 12$? Какое из боковых ребер пересекает в этом случае плоскость и на какие части его делит?

Решение:

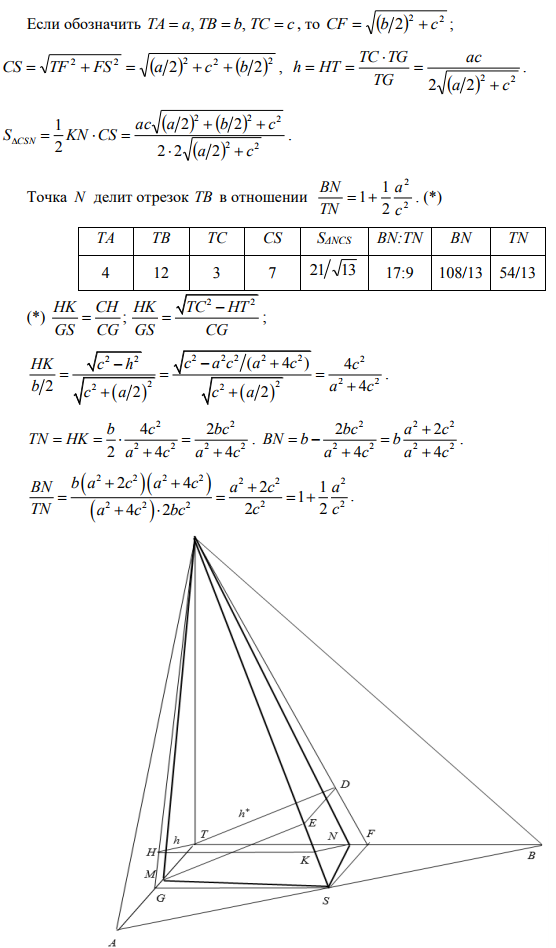
Задание добавил(а)

@slava191

Создатель и главный администратор проекта ExamMe.

О задание:

Источник условия: Второй (заключительный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по образовательному предмету «Математика», весна 2017 г.
Источник решения: Тот же, что и решения

Обсуждения

Только зарегистрированные пользователи могут оставлять комментарии.

Написать комментарий