ЕГЭ по Физике
Длинная узкая пластина массой $m$...
Задание:
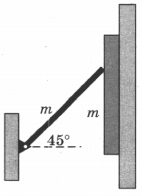
Длинная узкая пластина массой $m$ скользит вдоль вертикальной стенки. Пластина прижимается к стенке однородным жестким стержнем такой же массы $m$ (см. рисунок). Другой конец стержня закреплен в шарнире так, что стержень составляет с горизонтом постоянный угол 45°. Коэффициент трения между пластиной и стенкой $\mu_1 = 0,2$. Каким должен быть коэффициент трения между пластиной и стержнем, чтобы пластина двигалась равномерно?
Решение:
Дано:
$\alpha = 45^{\circ}$
$\mu_1 = 0,2$
Найти: $\mu_2$
Решение:
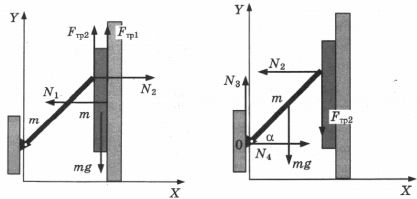
Сделаем рисунок, на котором покажем действующие на пластину силы: силу тяжести mg, силу реакции опоры стенки $N_1$, силу трения о стенку $F_{тр1}$, силу действия со стороны стержня $N_2$, силу трения пластины о стержень $F_{тр2}$. Для равномерного движения пластины необходимо, чтобы векторная сумма всех сил была равна О. Выберем координатные оси X и Y и спроецируем на них силы:
$OY: F_{тр1}+F_{тр2}-mg=0$
$OX: N_2+N_1=0$
Так как пластина скользит по стенке и стержень скользит по пластине, то силы трения скольжения равны произведению коэффициента трения на величину силы реакции опоры:
$F_{тр1} = \mu_1 N_1$ и $F_{тр2} = \mu_2 N_2$. Тогда $(\mu_1+\mu_2)N_1 = mg$
Далее рассмотрим силы, действующие на стержень: сила тяжести mg, сила реакции пластины $N_2$, сила трения скольжения о пластину $F_{тр2}$, силы реакции шарнира $N_3$ и $N_4$. По третьему закону Ньютона силы, действующие на стержень со стороны пластины, равны по модулю и противоположны по направлению силам, действующим на пластину со стороны стержня.
Положение стержня не меняется, следовательно, сумма моментов всех сил, на него действующих, равна 0. Рассмотрим моменты сил относительно оси, проходящей через точку 0 шарнира. Моменты сил $N_3$ и $N_4$ относительно этой оси равны нулю. Для остальных сил:
$mg\frac{l}{2}cos\alpha+F_{тр2}lcos\alpha-N_2lsin\alpha=0$, где $l$ — длина стержня. С учетом $F_{тр2}=\mu_2N_2$
$\alpha = 45^{\circ}$
$\mu_1 = 0,2$
Найти: $\mu_2$
Решение:
Сделаем рисунок, на котором покажем действующие на пластину силы: силу тяжести mg, силу реакции опоры стенки $N_1$, силу трения о стенку $F_{тр1}$, силу действия со стороны стержня $N_2$, силу трения пластины о стержень $F_{тр2}$. Для равномерного движения пластины необходимо, чтобы векторная сумма всех сил была равна О. Выберем координатные оси X и Y и спроецируем на них силы:
$OY: F_{тр1}+F_{тр2}-mg=0$
$OX: N_2+N_1=0$
Так как пластина скользит по стенке и стержень скользит по пластине, то силы трения скольжения равны произведению коэффициента трения на величину силы реакции опоры:
$F_{тр1} = \mu_1 N_1$ и $F_{тр2} = \mu_2 N_2$. Тогда $(\mu_1+\mu_2)N_1 = mg$
Далее рассмотрим силы, действующие на стержень: сила тяжести mg, сила реакции пластины $N_2$, сила трения скольжения о пластину $F_{тр2}$, силы реакции шарнира $N_3$ и $N_4$. По третьему закону Ньютона силы, действующие на стержень со стороны пластины, равны по модулю и противоположны по направлению силам, действующим на пластину со стороны стержня.
Положение стержня не меняется, следовательно, сумма моментов всех сил, на него действующих, равна 0. Рассмотрим моменты сил относительно оси, проходящей через точку 0 шарнира. Моменты сил $N_3$ и $N_4$ относительно этой оси равны нулю. Для остальных сил:
$mg\frac{l}{2}cos\alpha+F_{тр2}lcos\alpha-N_2lsin\alpha=0$, где $l$ — длина стержня. С учетом $F_{тр2}=\mu_2N_2$
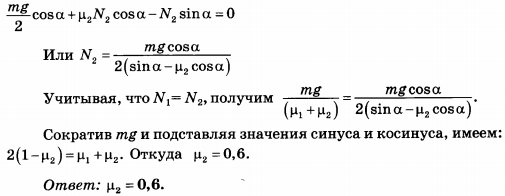
Задание добавил(а)
Создатель и главный администратор проекта ExamMe.
О задание:
Источник условия: Физика. Практикум. Экзаменационные тесты ЕГЭ 2017. С.Б. Бобошина.
Источник решения: Тот же, что и условия
Источник решения: Тот же, что и условия
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
