ОГЭ по Математике
Окружность с центром в точке...
Задание:
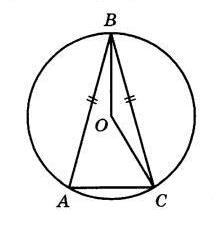
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором $AB=BC$ и $\angle ABC=28^{\circ}$(см. рис.). Найдите величину угла $\angle BOC$. Ответ дайте в градусах.
Решение:
Центр описанной около треугольника окружности - точка пересечения серединных перпендикуляров. Так как треугольник ABC равнобедренный, то серединный перпендикуляр к основанию(к стороне AC в данном случае), будет совпадать с медианой, биссектрисой и высотой. То есть радиус окружности $OB$ лежит на биссектрисе.
Тогда $\angle OBC=28^{\circ}:2=14^{\circ}$
Треугольник $BOC$-равнобедренный(OB и OC радиусы), значит, $\angle OBC=\angle OCB=14^{\circ}$.
Получаем, $\angle BOC=180^{\circ}-2\cdot 14^{\circ}=180^{\circ}-28^{\circ}=152^{\circ}$
Тогда $\angle OBC=28^{\circ}:2=14^{\circ}$
Треугольник $BOC$-равнобедренный(OB и OC радиусы), значит, $\angle OBC=\angle OCB=14^{\circ}$.
Получаем, $\angle BOC=180^{\circ}-2\cdot 14^{\circ}=180^{\circ}-28^{\circ}=152^{\circ}$
Ответ:
152
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
