Укажите, какое из следующих числовых выражений имеет наибольшее значение:

1) $5\sqrt{2}$
2) $\frac{1}{2}:10^{-1}$
3) $8$
4) $(-3):(-\frac{1}{2}-0,1)$

Смотреть решение

Какому из данных промежутков принадлежит число $\frac{3}{7}$?

1) $[0,1; 0,2]$
2) $[0,2; 0,3]$
3) $[0,3; 0,4]$
4) $[0,4; 0,5]$

Смотреть решение

Значение какого из данных ниже выражений является числом иррациональным?


1) $\sqrt{18}\cdot \sqrt{8}$

2) $(\sqrt{22}-\sqrt{7})\cdot(\sqrt{22}+\sqrt{7})$

3) $\frac{\sqrt{44}}{\sqrt{11}}$

4) $\sqrt{8}-4\sqrt{2}$

Смотреть решение

Найдите корень уравнения $10(x+2)=-7$.

Смотреть решение

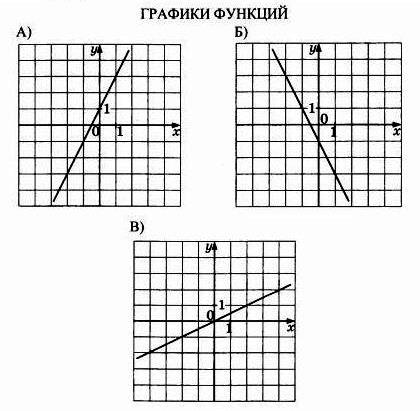
Установите соответствие меду графиками функций и формулами, которые их задают.
Графики функций представлены на рисунке.
Формулы:

1) $y=2x+1$

2) $y=\frac{x}{2}$

3) $y=-\frac{x}{2}$

4) $y=-2x-1$

Смотреть решение

Последовательность $(b_{n})$ задана условиями $b_{1}=-6$, $b_{n+1}=-2\cdot \frac{1}{b_{n}}$. Найдите $b_{5}$.

Смотреть решение

Найдите значение выражения $\frac{x^{11}x^{-4}}{x^{8}}$ при $x=0,4$.

Смотреть решение

Укажите решение неравенства $-3-3x > 7x-9$.

1) $(0,6; +\infty)$
2) $(-\infty; 1,2)$
3) $(1,2; +\infty)$
4) $(-\infty; 0,6)$

Смотреть решение

Катеты прямоугольного треугольника равны $60$ и $80$. Найдите гипотенузу этого треугольника.

Смотреть решение

В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $AB=\sqrt{2}AC$, $BC=6$.
Найдите высоту $CH$. В ответ запишите, чему равно $\sqrt{2}CH$.

Смотреть решение

В прямоугольном треугольнике один из катетов равен $\sqrt[4]{3}$, а угол, лежащий напротив него, равен 30°. Найдите площадь треугольника.

Смотреть решение

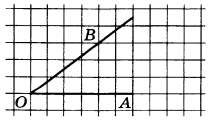
Найдите синус угла $AOB$, изображенного на рисунке

Смотреть решение

Укажите номера верных утверждений.

1) Скалярное произведение векторов равно произведению их длин на косинус угла между ними.
2) Длина суммы двух векторов равна сумме их длин.
3) Сумма внутренних накрест лежащих углов при пересечении двух параллельных прямых секущей равна 180 градусов.
4) Длина окружности равна ее удвоенному радиусу.
5) Площадь прямоугольника равна его периметру.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

Смотреть решение

В таблице приведен норматив по бегу на 800 метров для учащихся 9 классов.

Какую отметку получит мальчик, пробежавший эту дистанцию за 2 минуты и 37 секунд?

1) Отметка «5»
2) Отметка «4»
3) Отметка «3»
4) Норматив не выполнен

Смотреть решение

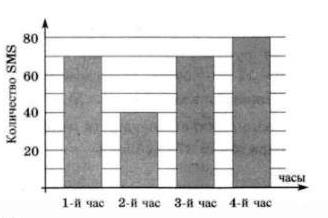
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.

Смотреть решение

Тест по математике содержит 36 заданий, причем задания по алгебре и геометрии содержатся в тесте в отношении 7 : 5. Сколько заданий по геометрии содержит данный тест?

Смотреть решение

Какой наименьший угол (в градусах) образуют минутная и часовая стрелки в 16:00?

Смотреть решение

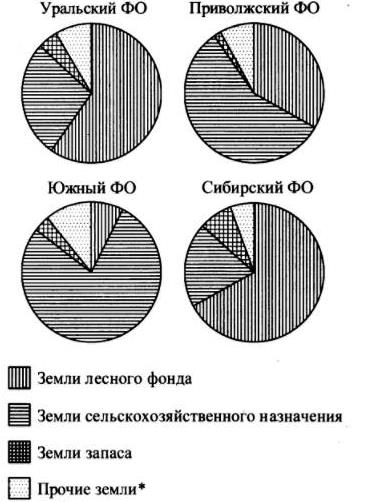
На диаграмме показано распределение земель по категориям Уральского, Приволжского, Южного и Сибирского федеральных округов. Определите по диаграмме, в каком округе доля земель лесного фонда наименьшая.

*Прочие земли - это земли поселений; земли промышленности и иного назначения; земли особо охраняемых территорий и объектов.

1) Уральский ФО
2) Приволжский ФО
3) Южный ФО
4) Сибирский ФО

Смотреть решение

На научной конференции будут выступать 3 докладчика из Германии, 2 из России и 5 из Японии. Найдите вероятность того, что последним будет выступать докладчик из России, если порядок выступления определяется жребием.

Смотреть решение

Площадь четырёхугольника можно вычислить по формуле $S=\frac{d_{1}d_{2}sin\alpha }{2}$, где $d_{1}$ и $d_{2}$ - длины диагоналей четырёхугольника, $\alpha$ - угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали $d_{2}$, если $d_{1}=6$, $sin\alpha =\frac{3}{7}$, а $S=18$.

Смотреть решение

Решите уравнение $x^3+3x^2=4x+12$

Смотреть решение

Теплоход проходит по течению реки до пункта назначения 132 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 21 час, а в пункт отправления теплоход возвращается через 32 часа после отплытия из него.

Смотреть решение

Постройте график функции $y=|3x-5|+|4x-7|$ и определите, при каких значениях p прямая y=p имеет с графиком ровно одну общую точку.

Смотреть решение

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=2, AC=8.

Смотреть решение

В выпуклом четырёхугольнике $ABCD$ углы $CDB$ и $CAB$ равны. Докажите, что углы $BCA$ и $BDA$ также равны.

Смотреть решение

В правильном шестиугольнике $ABCDEF$ со стороной $1$ найдите радиус окружности, вписанной в треугольник $ABC$.

Смотреть решение