ОГЭ по Математике
В равнобедренной трапеции основания...
Задание:
В равнобедренной трапеции основания равны $3$ и $7$, а один из углов между боковой стороной и основанием равен $45^{\circ}$. Найдите площадь трапеции.
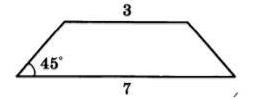
Решение:
Площадь трапеции найдём по формуле $S=\frac{a+b}{2}\cdot h$, где $a, b$ - основания трапеции, $h$ - высота.
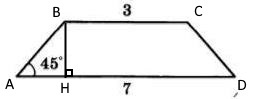
Обозначим трапецию $ABCD$ и опустим высоту $BH$(см. рис.).
Так как угол $BAH$ равен $45$ градусов(по условию), $BH$-высота, то треугольник $ABH$- равнобедренный и $AH=BH$.
Так как трапеция равнобедренная, то $AH=(AD-BC):2=(7-3):2=4:2=2$
Получаем, $BH=AH=h=2$
Тогда $S=\frac{3+7}{2}\cdot 2=5\cdot 2=10$
Обозначим трапецию $ABCD$ и опустим высоту $BH$(см. рис.).
Так как угол $BAH$ равен $45$ градусов(по условию), $BH$-высота, то треугольник $ABH$- равнобедренный и $AH=BH$.
Так как трапеция равнобедренная, то $AH=(AD-BC):2=(7-3):2=4:2=2$
Получаем, $BH=AH=h=2$
Тогда $S=\frac{3+7}{2}\cdot 2=5\cdot 2=10$
Ответ:
10
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
