ОГЭ по Математике
Сторона ромба равна $12$, а...
Задание:
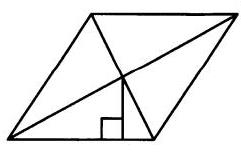
Сторона ромба равна $12$, а расстояние от точки пересечения диагоналей ромба до неё равно $4$. Найдите площадь ромба.
Решение:
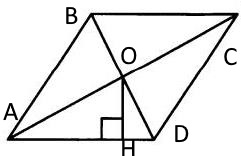
Обозначим ромб $ABCD$, $O$-точка пересечения диагоналей, $OH$-расстояние от точки пересечения диагоналей до стороны ромба(перпендикуляр опущенный из точки пересечения диагоналей на сторону ромба).
Диагонали ромба делят ромб на 4 равных треугольника, поэтому площадь ромба можно найти как 4 площади треугольника $AOD$.
Площадь треугольника можно найти, как полупроизведение стороны умноженной на высоту, проведенную к этой стороне.
Тогда, $S_{AOD}=\frac{1}{2}\cdot AD\cdot OH=\frac{1}{2}\cdot 12\cdot 4=24$
Площадь ромба равна $S=4\cdot 24=96$
Диагонали ромба делят ромб на 4 равных треугольника, поэтому площадь ромба можно найти как 4 площади треугольника $AOD$.
Площадь треугольника можно найти, как полупроизведение стороны умноженной на высоту, проведенную к этой стороне.
Тогда, $S_{AOD}=\frac{1}{2}\cdot AD\cdot OH=\frac{1}{2}\cdot 12\cdot 4=24$
Площадь ромба равна $S=4\cdot 24=96$
Ответ:
96
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
