ОГЭ по Математике
Основания трапеции равны $1$ и $17$....
Задание:
Основания трапеции равны $1$ и $17$. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
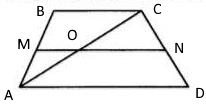
Обозначим трапецию $ABCD$, $MN$-средняя линия, $O$-точка пересечения средней линии и диагонали AC.
Средняя линия параллельна основаниям, тогда, по теореме Фалеса, $O$-так же является серединой $AC$.
Значит, $MO$-средняя линия для треугольника $CAB$ и $MO$ равно половине $BC$, то есть $MO=1:2=0,5$
$NO$-средняя линия для треугольника $ACD$ и $NO$ равно половине $AD$, то есть $NO=17:2=8,5$
Средняя линия параллельна основаниям, тогда, по теореме Фалеса, $O$-так же является серединой $AC$.
Значит, $MO$-средняя линия для треугольника $CAB$ и $MO$ равно половине $BC$, то есть $MO=1:2=0,5$
$NO$-средняя линия для треугольника $ACD$ и $NO$ равно половине $AD$, то есть $NO=17:2=8,5$
Ответ:
8,5
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
