Постройте график функции...

Постройте график функции $y=\frac{1}{2}(\left | \frac{x}{6}-\frac{6}{x} \right |+\frac{x}{6}+\frac{6}{x})$.

и определите, при каких при каких значениях $m$ прямая $y=m$ имеет с графиком ровно одну общую точку.

При $\frac{x}{6}-\frac{6}{x}\geq 0$

То есть при $x\in [-6; 0)\cup [6;+\infty)$ функция принимает вид:

$y=\frac{x}{6}$-линейная функция, графиком является прямая,ограниченная промежутками $x\in [-6; 0)\cup [6;+\infty)$ и проходящая через точки $(-6;-1), (-1;-\frac{1}{6}), (6;1), (12;2)$.

При $\frac{x}{6}-\frac{6}{x} < 0$

То есть при $x\in (-\infty; -6)\cup (0;6)$ функция принимает вид:

$y=\frac{6}{x}$ - обратная пропорциональность. Графиком является гипербола, ограниченная промежутками $x\in (-\infty; -6)\cup (0;6)$ и проходящая через точки $(-12; -\frac{1}{2}), (-8; -\frac{3}{4}), (1; 6), (2; 3), (3; 2)$

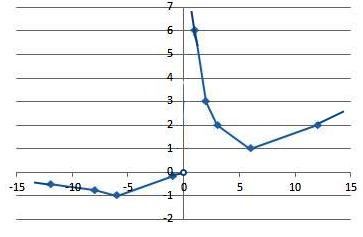
Построим график функции(см. рис.).

По рисунку видим, что при $m=-1$ и при $m=1$ прямая $y=m$ имеет с графиком ровно одну общую точку.