Постройте график функции...

Постройте график функции $y=\frac{4|x|-1}{|x|-4x^{2}}$ и определите, при каких значениях $k$ прямая $y=kx$ не имеет с графиком ни одной общей точки.

$y=\frac{4|x|-1}{|x|-4x^{2}}$

При $x\geq 0$ функция принимает вид:

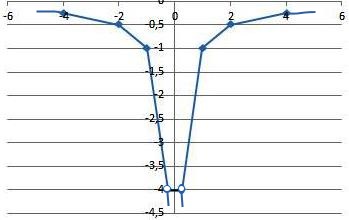
$y=-\frac{1}{x}$-обратная пропорциональность, графиком будет являться одна ветвь гиперболы, расположенная в четвертой четверти, с выколотой точкой $x=\frac{1}{4}$. График будет проходить через точки: $(1; -1), (2; -0,5), (4; -0,25)$.

При $x < 0$ функция принимает вид:

$y=\frac{1}{x}$-обратная пропорциональность, графиком будет являться одна ветвь гиперболы, расположенная в третьей четверти, с выколотой точкой $x=-\frac{1}{4}$. График будет проходить через точки: $(-1; -1), (-2; -0,5), (-4; -0,25)$.

Построим график функции(см. рис.)

$y=kx$ - прямая пропорциональность, графиком является прямая, проходящая через начало координат.

Получаем, при $k=0$ прямая $y=kx$ не имеет с графиком ни одной общей точки.

Так же, если прямая $y=kx$ будет проходить через выколотые точки графика, то так же не будет иметь с графиком ни одной общей точки.

Возьмём первую выколотую точку $(\frac{1}{4}; -4)$, если график функции $y=kx$ проходит через эту точку, то $k=-16$.

Вторая выколотая точка $(-\frac{1}{4}; -4)$, если график функции $y=kx$ проходит через эту точку, то $k=16$.

Ответ: $-16; 0; 16$.