ОГЭ по Математике
Расстояние от точки пересечения ...
Задание:
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
Решение:
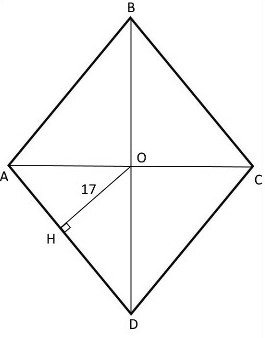
Сделаем рисунок, обозначим ромб $ABCD$, $O$-точка пересечения диагоналей, $OH=17$-расстояние от точки пересечения диагоналей ромба до одной из его сторон.
Пусть $BD=68$, тогда $OD=68:2=34$.
Значит, в прямоугольном треугольнике $OHD$: гипотенуза $OD=34$, а один катет равен $OH=17$, что в два раза меньше гипотенузы. Откуда получаем, угол $ODH=30^{\circ}$.
Тогда угол ромба $ADC=2\cdot 30^{\circ}=60^{\circ}$
Соответственно, угол $ABC$ равен углу $ADC=60^{\circ}$
И угол $DAB$ равен углу $DCB=180^{\circ}-60^{\circ}=120^{\circ}$
Ответ: $60^{\circ}$, $120^{\circ}$
Пусть $BD=68$, тогда $OD=68:2=34$.
Значит, в прямоугольном треугольнике $OHD$: гипотенуза $OD=34$, а один катет равен $OH=17$, что в два раза меньше гипотенузы. Откуда получаем, угол $ODH=30^{\circ}$.
Тогда угол ромба $ADC=2\cdot 30^{\circ}=60^{\circ}$
Соответственно, угол $ABC$ равен углу $ADC=60^{\circ}$
И угол $DAB$ равен углу $DCB=180^{\circ}-60^{\circ}=120^{\circ}$
Ответ: $60^{\circ}$, $120^{\circ}$
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
