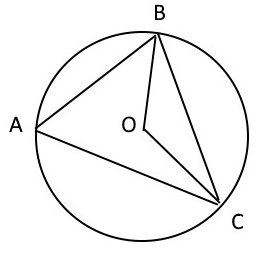
Углы $B$ и $C$ треугольника $ABC$...

Углы $B$ и $C$ треугольника $ABC$ равны соответственно $71^{\circ}$ и $79^{\circ}$. Найдите $BC$, если радиус окружности, описанной около треугольника $ABC$, равен $8$.

$O$-центр окружности, описанной около треугольника $ABC$.

Если углы $B$ и $C$ треугольника $ABC$ равны соответственно $71^{\circ}$ и $79^{\circ}$, то угол $A$ равен

$180^{\circ}-71^{\circ}-79^{\circ}=30^{\circ}$

Угол $A$ - вписанный угол, значит, центральный угол опирающийся на ту же дугу, будет в два раза больше.

То есть угол $BOC=2\cdot 30^{\circ}=60^{\circ}$

Треугольник $BOC$-равнобедренный(BO и OC радиусы) с основанием $BC$. Так как угол, лежащий напротив основания равен $60^{\circ}$, то и углы при основании равны по $60^{\circ}$.

Значит, $BOC$-равносторонний и $BC=BO=OC$, то есть равен радиусу.

Получаем, $BC=8$