Отрезки AB и CD являются хордами...

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояние от центра окружности до хорд AB и CD равны соответственно 12 и 9.

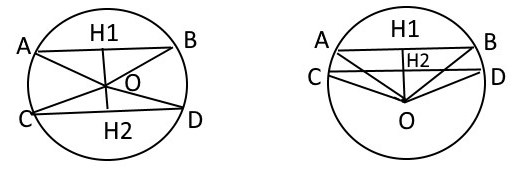
Заметим, что решение задачи не будет зависеть от расположения хорд(по разные или по одну сторону они будут находится от центра $O$ окружности)(См. рис.)

$OH1$-расстояние от центра окружности до хорды $AB$. Тогда $H1B=18:2=9$.

По теореме Пифагора из треугольника $OBH1$:

$OB=\sqrt{12^{2}+8^{2}}=15$

То есть радиус равен 15.

Тогда по теореме Пифагора из треугольника $ODH2$:

$H2D=\sqrt{15^{2}-9^{2}}=12$

Значит, $CD=2\cdot 12=24$