Окружность с центром на стороне AC...

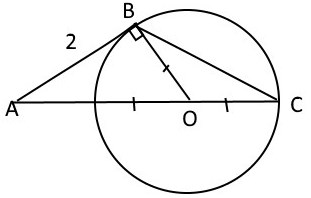
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=2, AC=8.

$OB=OC=R$

Так как $AB$ - касательная, $OB$ перпендикулярна $AB$.

Тогда треугольник $ABO$ прямоугольный.

По условию $AC=8$. Тогда $AO=8-R$

По теореме Пифагора из треугольника $ABO$:

$AO^{2}=AB^{2}+OB^{2}$

$(8-R)^{2}=2^{2}+R^{2}$

=> $R=3,75$

$D=2\cdot 3,75=7,5$