ОГЭ по Математике
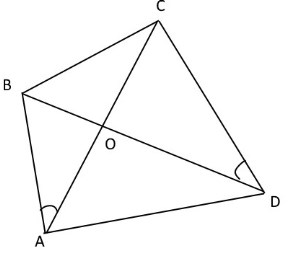
В выпуклом четырёхугольнике $ABCD$...
Задание:
В выпуклом четырёхугольнике $ABCD$ углы $CDB$ и $CAB$ равны. Докажите, что углы $BCA$ и $BDA$ также равны.
Решение:
$O$ - точка пересечения диагоналей $AC$ и $BD$.
В треугольниках $COD$ и $BOA$: углы $CDB$ и $CAB$ равны по условию, углы $COD$ и $BOA$ равны, как вертикальные.
Значит, треугольники $COD$ и $BOA$ подобны по двум углам.
Тогда $\frac{BO}{CO}=\frac{AO}{DO}$.
Получаем, что в треугольниках $COB$ и $DOA$: две стороны пропорциональны($\frac{BO}{AO}=\frac{CO}{DO}$), а углы $COB$ и $DOA$ равны, как вертикальные. Значит, треугольники $COB$ и $DOA$ подобны по двум пропорциональным сторонам и углу между ними.
Из пропорциональности треугольников следует равенство углов: углы $BCA$ и $BDA$ также равны
В треугольниках $COD$ и $BOA$: углы $CDB$ и $CAB$ равны по условию, углы $COD$ и $BOA$ равны, как вертикальные.
Значит, треугольники $COD$ и $BOA$ подобны по двум углам.
Тогда $\frac{BO}{CO}=\frac{AO}{DO}$.
Получаем, что в треугольниках $COB$ и $DOA$: две стороны пропорциональны($\frac{BO}{AO}=\frac{CO}{DO}$), а углы $COB$ и $DOA$ равны, как вертикальные. Значит, треугольники $COB$ и $DOA$ подобны по двум пропорциональным сторонам и углу между ними.
Из пропорциональности треугольников следует равенство углов: углы $BCA$ и $BDA$ также равны
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
