Окружности с центрами $I$ и $J$ не...

Окружности с центрами $I$ и $J$ не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении $m:n$. Докажите, что диаметры этих окружностей относятся как $m:n$.

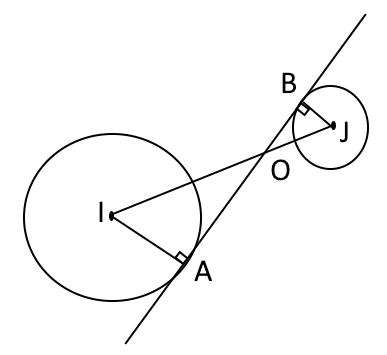
$A$ и $B$ - точки касания.

$O$ - точка пересечения касательной и отрезка, соединяющего центры окружностей $IJ$.

По условию: $IO:JO=m:n$

$IA$ и $JB$ - радиусы, проведенные в точки касания, т.е. они перпендикулярны касательной.

Углы $AOI$ и $BOJ$ равны, как вертикальные.

Треугольники $IAO$ и $JBO$ подобны по двум углам.

Значит, радиусы окружностей, соответственно и диаметры, относятся, как $m:n$.