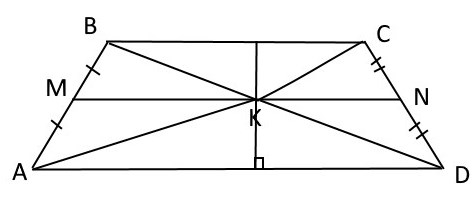
На средней линии трапеции $ABCD$ с...

На средней линии трапеции $ABCD$ с основаниями $AD$ и $BC$ выбрали произвольную точку $K$. Докажите, что сумма площадей треугольников $BKC$ и $AKD$ равна половине площади трапеции.

Площадь трапеции можно найти по формуле: $S_{tr}=\frac{AD+BC}{2}\cdot h$, где $h$ - высота трапеции

Площадь треугольника $BKC$ равна $S_{BKC}=\frac{1}{2}\cdot BC\cdot \frac{1}{2}h=\frac{1}{4}\cdot BC\cdot h$

Площадь треугольника $AKD$ равна $S_{AKD}=\frac{1}{2}\cdot AD\cdot \frac{1}{2}h=\frac{1}{4}\cdot AD\cdot h$

Тогда сумма площадей треугольников $BKC$ и $AKD$ равна

$S_{BKC}+S_{AKD}=\frac{1}{4}\cdot BC\cdot h+\frac{1}{4}\cdot AD\cdot h=\frac{1}{2}\cdot \frac{AD+BC}{2}\cdot h$, то есть половине площади трапеции