ОГЭ по Математике
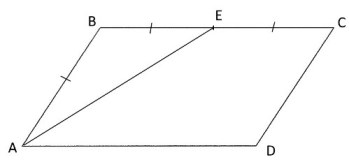
Сторона $BC$ параллелограмма $ABCD$...
Задание:
Сторона $BC$ параллелограмма $ABCD$ вдвое больше стороны $AB$. Точка $E$ - середина стороны $BC$. Докажите, что $AE$ - биссектриса угла $BAD$.
Решение:
Так как сторона $BC$ параллелограмма $ABCD$ вдвое больше стороны $AB$ и точка $E$ - середина стороны $BC$, то $AB=BE=EC$.
Тогда треугольник $ABE$ - равнобедренный с основанием $AE$.
И углы $BAE$ и $BEA$ равны.
Углы $EAD$ и $BEA$ равны, как накрестлежащие при параллельных прямых и секущей.
Получаем, что углы $BAE$ и $EAD$ равны, то есть $AE$ - биссектриса угла $BAD$.
Тогда треугольник $ABE$ - равнобедренный с основанием $AE$.
И углы $BAE$ и $BEA$ равны.
Углы $EAD$ и $BEA$ равны, как накрестлежащие при параллельных прямых и секущей.
Получаем, что углы $BAE$ и $EAD$ равны, то есть $AE$ - биссектриса угла $BAD$.
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
