В треугольнике $ABC$ биссектриса...

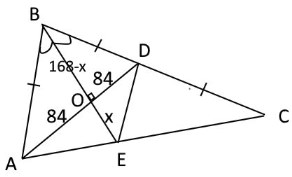
В треугольнике $ABC$ биссектриса $BE$ и медиана $AD$ перпендикулярны и имеют одинаковую длину, равную $168$. Найдите стороны треугольника $ABC$.

$O$ - точка пересечения $AD$ и $BE$.

Так как в треугольнике $ABD$: $BO$ является и биссектрисой, и высотой, то треугольник $ABD$ равнобедренный с основанием $AD$.

=> $AB=BD$, $AO=OD=168:2=84$

Треугольники $ABE$ и $DBE$ равны по двум сторонам и углу между ними($AB=BD$, $BE$-общая, углы $ABE$ и $DBE$ равны, т.к. $BE$-биссектриса)

=> $S_{ABE}=S_{DBE}=(\frac{1}{2}\cdot BE\cdot AD):2=(\frac{1}{2}\cdot 168\cdot 168):2=84\cdot 84$

Так как в треугольнике $BEC$: $ED$-медиана, то $S_{BED}=S_{CED}=84\cdot 84$

Тогда $S_{ABC}=3\cdot 84\cdot 84$

В треугольнике $ABC$: $AD$-медиана, значит $S_{ABD}=S_{ACD}=\frac{3\cdot 84\cdot 84}{2}=3\cdot 42\cdot 84$

Пусть $OE=x$, тогда $BO=168-x$

$S_{ABD}=\frac{1}{2}\cdot AD\cdot BO=\frac{1}{2}\cdot 168\cdot (168-x)=84(168-x)$

$84(168-x)=3\cdot 42\cdot 84$

$x=42$

Значит, $OE=42$, тогда $BO=168-42=126$

По теореме Пифагора из треугольника $BOA$:

$AB=\sqrt{126^{2}+84^{2}}=42\sqrt{13}$

=> $BC=2\cdot 42\sqrt{13}=84\sqrt{13}$

По теореме Пифагора из треугольника $AOE$:

$AE=\sqrt{42^{2}+84^{2}}=42\sqrt{5}$

Так как $BE$-биссектриса, то она делит сторону $AC$ в отношении $\frac{AB}{BC}=\frac{AE}{EC}$

=> $EC=\frac{BC\cdot AE}{AB}=\frac{84\sqrt{13}\cdot 42\sqrt{5}}{42\sqrt{13}}=84\sqrt{5}$

=> $AC=84\sqrt{5}+42\sqrt{5}=126\sqrt{5}$

Ответ: $AB=42\sqrt{13}$; $BC=84\sqrt{13}$; $AC=126\sqrt{5}$