Середина $M$ стороны $AD$ выпуклого...

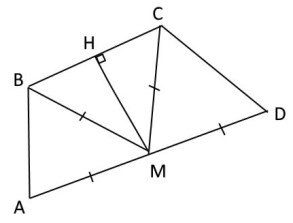
Середина $M$ стороны $AD$ выпуклого четырехугольника $ABCD$ равноудалена от всех его вершин. Найдите $AD$, если $BC=14$, а углы $B$, $C$ четырехугольника равны соответственно $110 ^{\circ}$ и $100 ^{\circ}$.

Так как точка $M$ равноудалена от всех вершин четырехугольника $ABCD$, то около этого четырехугольника можно описать окружность с центром в точке $M$.

=> Суммы противоположных углов четырехугольника $ABCD$ равны $180^{\circ}$

Значит, угол $BAD=180^{\circ}-100^{\circ}=80^{\circ}$

Угол $CDA=180^{\circ}-110^{\circ}=70^{\circ}$

Треугольник $AMB$ равнобедренный с основанием $AB$ ($AM=BM=R$)

=> угол $MAB$ равен углу $ABM=80^{\circ}$

Тогда угол $MBC=110^{\circ}-80^{\circ}=30^{\circ}$

Треугольник $BMC$ так же равнобедренный ($BM=CM=R$) с основанием $BC$

$MH$-и медиана, и высота.

$BH=14:2=7$

Из прямоугольного треугольника $BHM$:

$cos MBH=\frac{BH}{BM}$

$cos 30^{\circ}=\frac{7}{BM}$

$\frac{\sqrt{3}}{2}=\frac{7}{BM}$

$BM=\frac{14\sqrt{3}}{3}$

$BM=AM=MD=\frac{14\sqrt{3}}{3}$

=> $AD=2\cdot \frac{14\sqrt{3}}{3}=\frac{28\sqrt{3}}{3}$