Постройте график функции $y=|x-4|+7$...

Постройте график функции $y=|x-4|+7$ и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком ровно одну общую точку.

Построим график функции $y=|x-4|+7$. Для этого рассмотрим два случая: когда выражение, стоящее под знаком модуля, больше или равно нулю и когда оно меньше нуля.

1. $x-4\geqslant0$
То есть $x\geq 4$

Тогда, снимаем модуль с положительным знаком и функция примет вид:

$y=x-4+7$
$y=x+3$

Это линейная функция, графиком будет являться прямая, проходящая через точки $(5; 8)$ и $(6; 9)$.

2. $x-4<0$
То есть $x<4$

Тогда, снимаем модуль с отрицательным знаком и функция примет вид:

$y=-(x-4)+7$
$y=-x+4+7$
$y=-x+11$

Это линейная функция, графиком будет являться прямая, проходящая через точки $(3; 8)$ и $(2; 9)$.

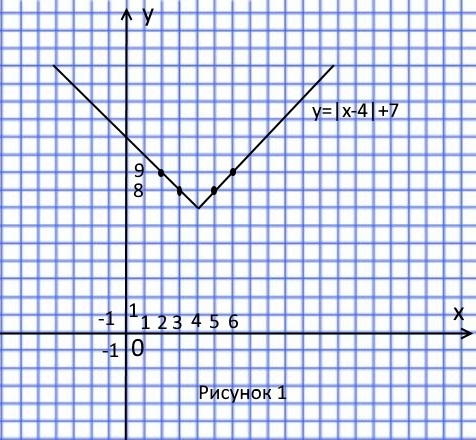
График функции представлен на рисунке 1.

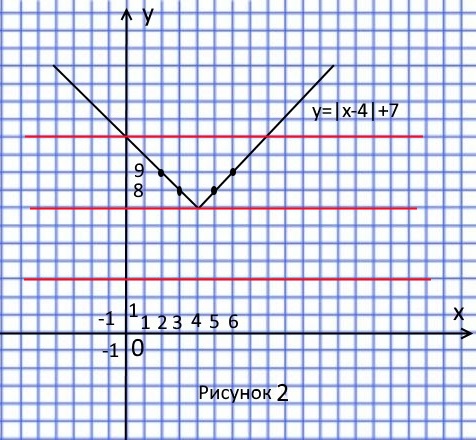
На рисунке 2 показано, что при $p>7$ прямая $y=p$ имеет с графиком две общие точки.
При $p<7$ прямая $y=p$ не имеет с графиком общих точек.
При $p=7$ прямая $y=p$ имеет с графиком ровно одну общую точку.
Значит, $p=7$