ОГЭ по Математике
В треугольнике ABC проведены медианы...
Задание:
В треугольнике ABC проведены медианы AK и BM, пересекающиеся в точке O. Докажите, что площади треугольников MOK и AOB относятся как 1:4.
Решение:
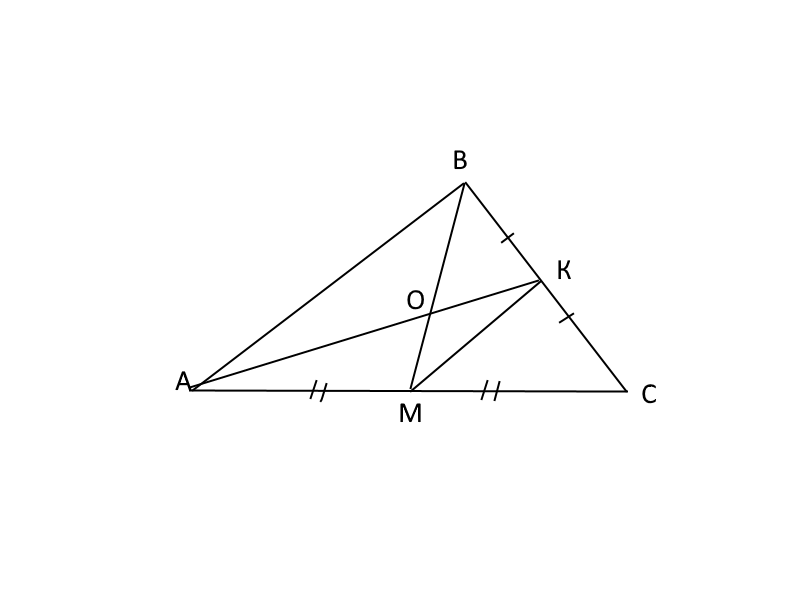
Сделаем рисунок.
Так как AK и BM медианы, то точка О делит их в отношении 2:1, считая от вершины.
АК - средняя линия треугольника АВС, => $AK=\frac{1}{2}AB$.
Значит, треугольник ОАК подобен треугольнику ОВА по трем пропорциональным сторонам. Коэффициент подобия $k=\frac{1}{2}$.
Тогда площади треугольников ОАК и ОВА относятся, как коэффициент подобия в квадрате, т.е. 1 к 4.
Так как AK и BM медианы, то точка О делит их в отношении 2:1, считая от вершины.
АК - средняя линия треугольника АВС, => $AK=\frac{1}{2}AB$.
Значит, треугольник ОАК подобен треугольнику ОВА по трем пропорциональным сторонам. Коэффициент подобия $k=\frac{1}{2}$.
Тогда площади треугольников ОАК и ОВА относятся, как коэффициент подобия в квадрате, т.е. 1 к 4.
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Новый сборник заданий ОГЭ2017. Л.Д. Лапоо, М.А. Попов.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
