Решите неравенство $2(x-1)(x+2)\leq...

Решите неравенство $2(x-1)(x+2)\leq 0$.

В ответе укажите количество целых решений данного неравенства.

$2(x-1)(x+2)\leq 0$

Найдем нули функции(значения $x$, при которых значение выражения $2(x-1)(x+2)$ равно нулю):

$2(x-1)(x+2)=0$

Данное произведение равно нулю, при $x-1=0$, то есть при $x=1$ или при $x+2=0$, то есть при $x=-2$.

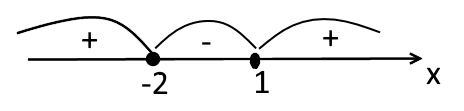
Отметим полученные значения на координатной прямой и определим знаки на каждом промежутке(см. рис.).
Для определения знаков на каждом промежутке, возьмем конкретное значение, принадлежащее выбранному промежутку и подставим в данное выражение:

При х=-3, получим: 2(-3-1)(-3+2)=2(-4)(-1)=8 > 0

При х=0, получим: 2(0-1)(0+2)=2(-1)*2=-4 < 0

При х=2, получим: 2(2-1)(2+2)=2*1*4=8 > 0

Так как неравенство нестрогое(меньше либо равно нулю), выбираем промежуток:

$x\in [-2; 1]$

Целые значения на данном отрезке: -2, -1, 0, 1. То есть 4 целых значения.