В треугольнике $ABC$ угол $C$ равен...

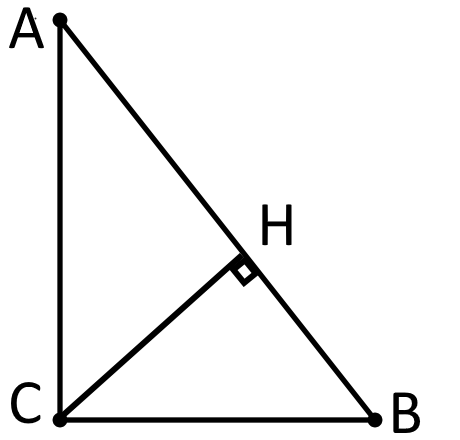
В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $AB=\sqrt{2}AC$, $BC=6$.
Найдите высоту $CH$. В ответ запишите, чему равно $\sqrt{2}CH$.

Пусть $AC=x$, тогда $AB=\sqrt{2}x$.

По теореме Пифагора из треугольника $ABC$, получим:

$AC^{2}+BC^{2}=AB^{2}$
$x^{2}+6^{2}=(\sqrt{2}x)^{2}$
$x^{2}+36=2x^{2}$
$2x^{2}-x^{2}=36$
$x^{2}=36$
$x^{2}=6$ (Так как по условию задачи, х - сторона треугольника, значение $х=-6$ исключаем)

Значит, $AC=6$, тогда $AB=6\sqrt{2}$.

$AC=BC=6$, => треугольник $ABC$ равнобедренный с основанием $AB$ и высота $HB$ является еще и медианой, то есть $AH=HB=6\sqrt{2}:2=3\sqrt{2}$

Пусть $CH=y$.

По теореме Пифагора из треугольника $CHB$, получим:

$CH^{2}+BH^{2}=CB^{2}$
$y^{2}+(3\sqrt{2})^{2}=6^{2}$
$y^{2}+9*2=36$
$y^{2}=36-18$
$y^{2}=18$
$y=\sqrt{18}=3\sqrt{2}$ (Так как по условию задачи, х - сторона треугольника, значение $х=-3\sqrt{2}$ исключаем)

Значит, $CH=3\sqrt{2}$.
Тогда $\sqrt{2}CH=\sqrt{2}*3\sqrt{2}=3*2=6$