ОГЭ по Математике
В треугольнике ABC стороны равны 3,...
Задание:
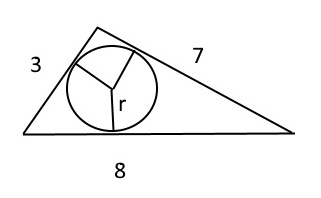
В треугольнике ABC стороны равны 3, 7 и 8. Найдите радиус окружности, вписанной в треугольник.
Решение:
Радиус вписанной в треугольник окружности находится по формуле:
$r=\frac{S}{p}$, где S-площадь треугольника, а p-полупериметр.
$p=\frac{a+b+c}{2}$, здесь и далее a, b, c - стороны треугольника.
$p=\frac{3+7+8}{2}=\frac{18}{2}=9$
Зная, все стороны треугольника площадь можно найти по формуле Герона:
$S=\sqrt{p(p-a)(p-b)(p-c)}$
$S=\sqrt{9(9-3)(9-7)(9-8)}=\sqrt{9\cdot 6\cdot 2\cdot 1}=6\sqrt{3}$
Тогда $r=\frac{6\sqrt{3}}{9}=\frac{2\sqrt{3}}{3}$
$r=\frac{S}{p}$, где S-площадь треугольника, а p-полупериметр.
$p=\frac{a+b+c}{2}$, здесь и далее a, b, c - стороны треугольника.
$p=\frac{3+7+8}{2}=\frac{18}{2}=9$
Зная, все стороны треугольника площадь можно найти по формуле Герона:
$S=\sqrt{p(p-a)(p-b)(p-c)}$
$S=\sqrt{9(9-3)(9-7)(9-8)}=\sqrt{9\cdot 6\cdot 2\cdot 1}=6\sqrt{3}$
Тогда $r=\frac{6\sqrt{3}}{9}=\frac{2\sqrt{3}}{3}$
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Новый сборник заданий ОГЭ2017. Л.Д. Лапоо, М.А. Попов.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
