ОГЭ по Математике
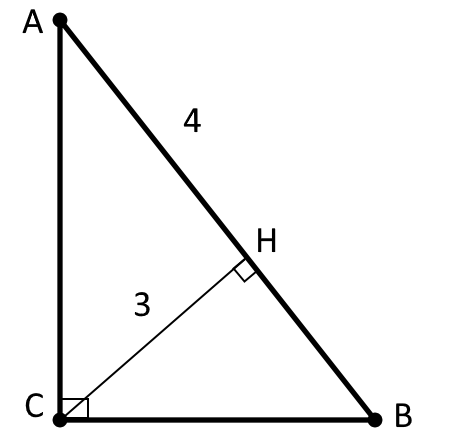
В треугольнике $ABC$ угол $C$ равен...
Задание:
В треугольнике $ABC$ угол $C$ равен $90^{\circ}$, $CH$-высота, $AH=4$, $CH=3$. Найдите $BC$.
Решение:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза высотой.
$CH=\sqrt{AH\cdot HB}$
$CH^{2}=AH\cdot HB$
=> $HB=\frac{CH^{2}}{AH}$
$HB=\frac{3^{2}}{4}=\frac{9}{4}$
При этом катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла:
$BC=\sqrt{AB\cdot HB}$
$BC=\sqrt{(4+\frac{9}{4})\cdot \frac{9}{4}}$
$BC=\sqrt{9+\frac{81}{16}}=\sqrt{\frac{144+81}{16}}=$
$=\sqrt{\frac{225}{16}}=\frac{15}{4}=3,75$
$CH=\sqrt{AH\cdot HB}$
$CH^{2}=AH\cdot HB$
=> $HB=\frac{CH^{2}}{AH}$
$HB=\frac{3^{2}}{4}=\frac{9}{4}$
При этом катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла:
$BC=\sqrt{AB\cdot HB}$
$BC=\sqrt{(4+\frac{9}{4})\cdot \frac{9}{4}}$
$BC=\sqrt{9+\frac{81}{16}}=\sqrt{\frac{144+81}{16}}=$
$=\sqrt{\frac{225}{16}}=\frac{15}{4}=3,75$
Ответ:
3,75
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: Новый сборник заданий ОГЭ2017. Л.Д. Лапоо, М.А. Попов.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
