Постройте график функции...

Постройте график функции $y=|2x-5|+|2x+8|+4$ и определите, при каких значениях p прямая y=p не имеет с графиком общих точек.

$y=|2x-5|+|2x+8|+4$

Подмодульные выражения равны нулю при $x=2,5$ и $x=-4$.
Эти две точки разбивают координатную прямую на 3 промежутка.

На промежутке $(-\infty;-4)$ оба подмодульных выражения отрицательны, значит, снимаем модули со знаком минус. Функция принимает вид:

$y=-(2x-5)-(2x+8)+4$
$y=-2x+5-2x-8+4$
$y=-4x+1$

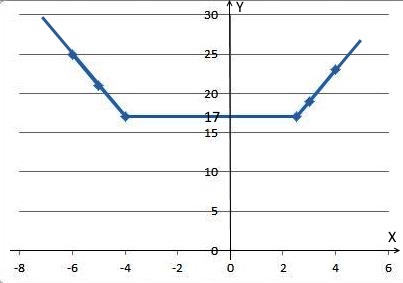
Линейная функция, графиком является прямая, проходящая через точки $(-5; 21)$ и $(-6; 25)$.

На промежутке $[-4;2,5]$ первое подмодульное выражение отрицательное, его снимаем со знаком минус, второе - положительное, его снимаем со знаком плюс.
Функция принимает вид:

$y=-(2x-5)+(2x+8)+4$
$y=-2x+5+2x+8+4$
$y=17$

Линейная функция, графиком является прямая, проходящая через точку $y=17$ параллельно оси $Ox$.

На промежутке $(2,5;+\infty)$ оба подмодульных выражения положительны, значит, снимаем модули со знаком плюс.
Функция принимает вид:

$y=2x-5+2x+8+4$
$y=4x+7$

Линейная функция, графиком является прямая, проходящая через точки $(3; 19)$ и $(4; 23)$.

Построим график функции(см. рис.)

При $p < 17$ прямая y=p не имеет с графиком общих точек.