Во сколько раз радиус окружности,...

Во сколько раз радиус окружности, описанной около квадрата, больше радиуса окружности, вписанной в этот же квадрат?

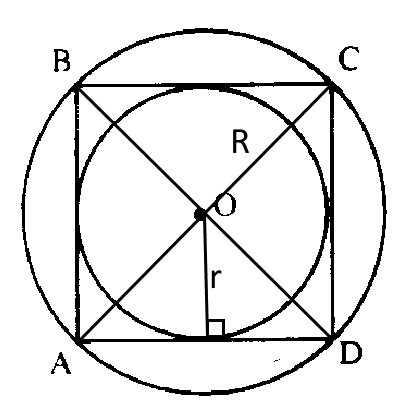
Пусть дан квадрат $ABCD$ со стороной $a$, $O$-точка пересечения диагоналей, она же будет являться центром вписанной и описанной окружностей(см. рис.).

Пусть $R$-радиус описанной окружности, $R=\frac{1}{2}AC$
Найдем $AC$ по теореме Пифагора из треугольника $ABC$:

$AC^{2}= AB^{2}+BC^{2}$
$AC^{2}= a^{2}+a^{2}$
$AC^{2}= 2a^{2}$
$AC=a\sqrt{2}$

Тогда, $R=\frac{1}{2}*a\sqrt{2}=\frac{a\sqrt{2}}{2}$

Если $r$-радиус вписанной окружности, то $r=\frac{1}{2}AB=\frac{1}{2}a=\frac{a}{2}$

$\frac{R}{r}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a}{2}}=\frac{a\sqrt{2}}{2}\cdot \frac{2}{a}=\sqrt{2}$