Найдите радиус окружности, вписанной...

Найдите радиус окружности, вписанной в правильный треугольник со стороной $\sqrt{3}$.

Радиус окружности вписанной в правильный треугольник можно найти по формуле $r=\frac{a\sqrt{3}}{6}$, где $a$ - сторона треугольника.

Тогда, радиус данной окружности будет равен

$r=\frac{\sqrt{3} \sqrt{3}}{6}=\frac{3}{6}=\frac{1}{2}=0,5$

Другое решение: Центр вписанной и описанной окружностей правильного треугольника - это центр треугольника, то есть точка пересечения биссектрис, медиан и высот.

Так как медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной окружности равен одной третьей медианы.

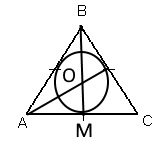
$BM$-медиана и высота, $OM$-радиус вписанной окружности(см. рис.).
Если $AC=\sqrt{3}$, то $MC=\frac{\sqrt{3}}{2}$
Тогда по теореме Пифагора из треугольника $BMC$:

$BM^{2}+MC^{2}=BC^{2}$

$BM^{2}=BC^{2}-MC^{2}$

$BM^{2}=(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}$

$BM^{2}=3-\frac{3}{4}$

$BM^{2}=\frac{9}{4}$

$BM=\frac{3}{2}$

Тогда радиус вписанной окружности равен $r=\frac{1}{3} \cdot \frac{3}{2}=\frac{1}{2}=0,5$