Постройте график функции...

Постройте график функции

$y=\left\{\begin{matrix}\frac{1}{x}, x<-1& & \\ |x^{2}|-2, x\geq -1 & & \end{matrix}\right.$

и определите, при каких значениях $p$ прямая $y=p$ имеет с графиком ровно одну общую точку.

$y=\frac{1}{x}, x<-1$ - обратная пропорциональность, графиком является гипербола, ограниченная по $x$: $x<-1$.

Проходит через точки $(-2; -\frac{1}{2})$, $(-3; -\frac{1}{3})$, $(-4; -\frac{1}{4})$.

$y=|x^{2}|-2, x\geq -1$ - квадратичная функция, графиком является парабола, ограниченная по $x$: $x\geq -1$.

Вершина параболы имеет координаты:

$x_{0}=\frac{-b}{2a}=\frac{0}{1}=0$

$y_{0}=0-2=-2$

Парабола проходит через точки: $(-1; -1)$, $(1; -1)$, $(2; 2)$, $(3; 7)$

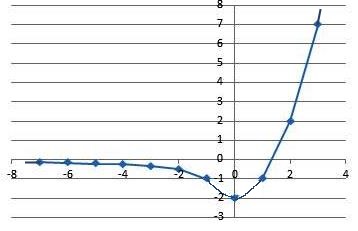
Построим график функции(см. рис.).

При $p=-2$ и при $p\geq 0$ прямая $y=p$ имеет с графиком ровно одну общую точку.