Трапеция вписана в окружность, ее...

Трапеция вписана в окружность, ее боковая сторона равна 3, а основания - 4 и 7. Найдите ее площадь.

Площадь трапеции равна $S=\frac{a+b}{2}\cdot h$, где a,b-основания трапеции, h-высота.

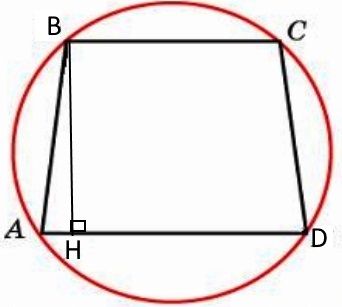
Так как трапеция ABCD вписана в окружность (см. рис.), то она равнобедренная.

Опустим высоту BH.

$AH=\frac{AD-BC}{2}$ (по свойству равнобедренной трапеции)

$AH=\frac{7-4}{2}=\frac{3}{2}$

По теореме Пифагора из треугольника $ABH$: $BH=\sqrt{AB^{2}-AH^{2}}$

$BH=\sqrt{3^{2}-(\frac{3}{2})^{2}}=\sqrt{9-\frac{9}{4}}=\frac{3\sqrt{3}}{2}$

Тогда $S=\frac{4+7}{2}\cdot \frac{3\sqrt{3}}{2}=\frac{33\sqrt{3}}{4}$