В правильном шестиугольнике $ABCDEF$...

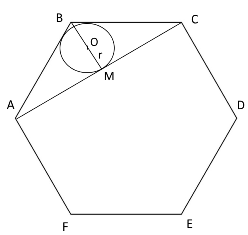
В правильном шестиугольнике $ABCDEF$ со стороной $1$ найдите радиус окружности, вписанной в треугольник $ABC$.

Радиус вписанной окружности находится по формуле $r=\frac{2S}{P}$, где $S$-площадь треугольника, $P$-его периметр.

По условию в треугольнике $ABC$: $AB=BC=1$. Так как дан правильный шестиугольник, то угол $ABC=720 : 6 = 120$ градусов, значит, угол $BCA$ = углу $BAC = (180-120):2=30$ градусов.

Опустим медиану $BM$, она же является и биссектрисой, и высотой.

Тогда в прямоугольном треугольнике $BMC$: $BM=BC:2=\frac{1}{2}$

По теореме Пифагора из этого же треугольника:

$MC=\sqrt{BC^{2}-BM^{2}}$

$MC=\sqrt{1^{2}-(\frac{1}{2}})^{2}=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}$

Тогда $AC=2MC=\frac{2\sqrt{3}}{2}=\sqrt{3}$

$S=\frac{1}{2}\cdot AC\cdot BM=\frac{1}{2}\cdot \sqrt{3}\cdot \frac{1}{2}=$

$=\frac{\sqrt{3}}{4}$

$P=AB+BC+AC=1+1+\sqrt{3}=2+\sqrt{3}$

$r=\frac{2\frac{\sqrt{3}}{4}}{2+\sqrt{3}}=\frac{\frac{\sqrt{3}}{2}}{2+\sqrt{3}}=$

$=\frac{\sqrt{3}}{2(2+\sqrt{3})}=\frac{\sqrt{3}}{4+2\sqrt{3}}=$

$=\frac{\sqrt{3}(4-2\sqrt{3})}{(4+2\sqrt{3})(4-2\sqrt{3})}=\frac{4\sqrt{3}-6}{4}=$

$=\frac{2\sqrt{3}-3}{2}$