ОГЭ по Математике
Четырехугольник ABCD вписан в...
Задание:
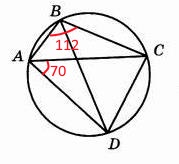
Четырехугольник ABCD вписан в окружность(см. рис.). Угол ABC равен $112^{\circ}$, угол CAD равен $70^{\circ}$. Найдите угол ABD. Ответ дайте в градусах.
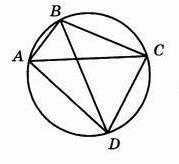
Решение:
По свойству четырехугольника, вписанного в окружность: Суммы противоположных углов равны $180^{\circ}$.
Значит, угол ADC равен $180^{\circ}-112^{\circ}=68^{\circ}$.
Тогда из треугольника ADC получаем, что угол $ACD=180^{\circ}-(70^{\circ}+68^{\circ})=42^{\circ}$.
Так как вписанные углы ACD и ABD опираются на одну и ту же дугу окружности, их градусные величины равны. То есть угол $ABD=42^{\circ}$
Значит, угол ADC равен $180^{\circ}-112^{\circ}=68^{\circ}$.
Тогда из треугольника ADC получаем, что угол $ACD=180^{\circ}-(70^{\circ}+68^{\circ})=42^{\circ}$.
Так как вписанные углы ACD и ABD опираются на одну и ту же дугу окружности, их градусные величины равны. То есть угол $ABD=42^{\circ}$
Ответ:
42
Задание добавил(а)
Редактор проекта ExamMe
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
