Задача №6.111
Условие
Пси-функция некоторой частицы имеет вид ψ=A ехр(-r2/2a2), где r — расстояние частицы от силового центра, a — константа. Найти:а) значение коэффициента A,
б) наиболее вероятное rвер и среднее <r> расстояния частицы от центра.
Решение
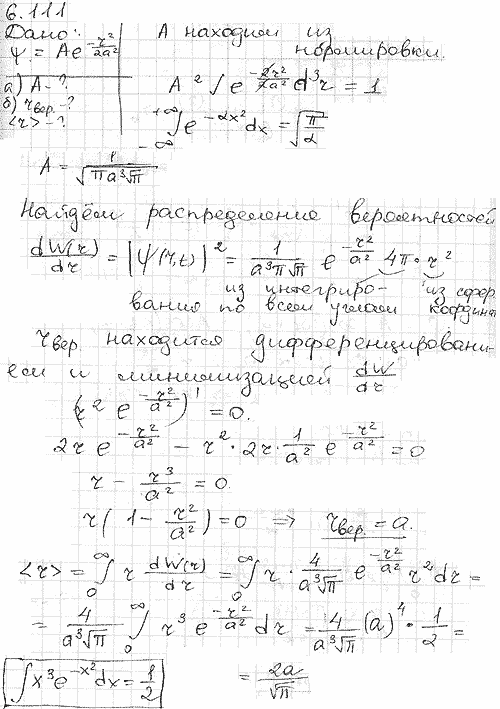
☆
Добавить в избранное

1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.20
1.21
1.22
1.23
1.24
1.25
1.26
1.28
1.29
1.30
1.31
1.33
1.34
1.35
1.36
1.37
1.38
1.39
1.40
1.41
1.42
1.44
1.47
1.48
1.55
1.56
1.57
1.58
1.59
1.60
1.61
1.62
1.63
1.64
1.65
1.66
1.67
1.68
1.69
1.72
1.73
1.74
1.75
1.76
1.77
1.78
1.79
1.80
1.81
1.82
1.83
1.84
1.85
1.86
1.87
1.89
1.90
1.91
1.92
1.93
1.94
1.95
1.96
1.99
1.100
1.101
1.102
1.103
1.104
1.105
1.106
1.107
1.108
1.114
1.115
1.116
1.117
1.118
1.119
1.122
1.123
1.124
1.125
1.126
1.127
1.137
1.139
1.141
1.147
1.148
1.149
1.150
1.152
1.153
1.154
1.155
1.160
1.165
1.168
1.170
1.180
1.185
1.187
1.189
1.190
1.191
1.192
1.195
1.196
1.198
1.214
1.215
1.218
1.219
1.220
1.221
1.222
1.223
1.237
1.243
1.252
1.256
1.259
1.260
1.267
1.271
1.273
1.275
1.276
1.277
1.278
1.280
1.281
1.283
1.284
1.285
1.287
1.288
1.289
1.291
1.292
1.293
1.294
1.298
1.305
1.318
1.320
1.322
1.328
1.329
1.333
1.341
1.343
1.345
2.6
2.9
2.15
2.23
2.25
2.31
2.33
2.41
2.42
2.43
2.44
2.45
2.56
2.63
2.66
2.68
2.69
2.70
2.71
2.72
2.77
2.78
2.80
2.83
2.84
2.85
2.87
2.88
2.93
2.95
2.96
2.97
2.99
2.109
2.122
2.126
2.135
2.136
2.137
2.138
2.140
2.154
2.157
2.159
2.162
2.165
2.166
2.168
2.169
2.176
2.180
2.186
2.188
2.189
2.190
2.192
2.198
2.199
2.200
2.208
3.3
3.5
3.6
3.9
3.12
3.15
3.16
3.17
3.18
3.19
3.20
3.21
3.23
3.27
3.28
3.30
3.36
3.38
3.40
3.41
3.42
3.44
3.45
3.52
3.53
3.55
3.59
3.60
3.61
3.62
3.63
3.64
3.65
3.66
3.69
3.70
3.71
3.77
3.78
3.79
3.82
3.84
3.85
3.88
3.97
3.104
3.105
3.106
3.109
3.114
3.117
3.124
3.127
3.128
3.131
3.141
3.143
3.144
3.145
3.147
3.149
3.157
3.159
3.161
3.163
3.164
3.168
3.169
3.171
3.175
3.176
3.178
3.179
3.180
3.183
3.184
3.185
3.186
3.187
3.189
3.190
3.191
3.192
3.193
3.196
3.197
3.198
3.199
3.201
3.202
3.203
3.206
3.208
3.209
3.210
3.213
3.214
3.215
3.216
3.225
3.234
3.240
3.242
3.244
3.249
4.5
4.12
4.15
4.17
4.25
4.29
4.34
4.39
4.42
4.49
4.51
4.52
4.55
4.56
4.57
4.58
4.60
4.61
5.3
5.11
5.18
5.31
5.34
5.35
5.36
5.38
5.39
5.44
5.45
5.46
5.47
5.48
5.56
5.59
5.63
5.65
5.67
5.69
5.70
5.72
5.78
5.83
5.86
5.93
5.100
5.108
5.111
5.120
5.122
5.124
5.125
5.129
5.136
5.138
5.145
5.150
5.152
5.154
5.155
5.158
5.159
5.163
5.166
5.171
6.3
6.8
6.10
6.15
6.19
6.21
6.22
6.24
6.32
6.36
6.44
6.45
6.49
6.55
6.60
6.62
6.63
6.67
6.68
6.72
6.75
6.80
6.81
6.82
6.86
6.87
6.90
6.92
6.93
6.95
6.96
6.97
6.98
6.99
6.102
6.103
6.104
6.105
6.107
6.108
6.111
6.114
6.117
6.118
6.120
6.121
6.123
6.125
6.126
6.127
6.128
6.129
6.135
6.136
6.142
6.144
6.146
6.147
6.149
6.175
6.184
6.199
6.200
6.201
6.202



